説明資料は「統計学」で味付けするとぐっと美味しくなる

世の中で統計学を知っている人とそうでない人の割合はどのくらいでしょうか。経験的には圧倒的多数は「知らない」人です。知っていたとしても小学校で習う「平均」ぐらいです。多数のデータを一言で表現する手段は多々あるのですが、多くの人が平均しか分かりませんので、結局伝える方も平均を使ってしまうということになります。

ですが、ここで「統計学」を使ってちょっと別の方法を使えば、あなたのプレゼン資料や報告書をぐっと美味しく味付けすることができます。説得力が増して、聞き手に感心してもらうことができるのです。

有意な変化とは

ある業務の品質に関するデータがあったとします。そして品質改善活動を行って、またその業務の品質に関するデータを取得したときに、どうすれば改善活動の効果があったといえるでしょうか？

ここで通常使われるのが、平均です。データを全部足して個数で割れば平均が求められます。例えば、不良品の個数の平均値が小さくなれば、改善活動の効果があった、ということになります。

本当でしょうか？たまたまかもしれませんよね？

ここで登場するのが「Ｔ検定」（てぃーけんてい）です。

T検定の意味

T検定とは、Wikipediaによると、次のように定義されています。

t検定（ティーけんてい）とは、帰無仮説が正しいと仮定した場合に、統計量がt分布に従うことを利用する統計学的検定法の総称である。母集団が正規分布に従うと仮定するパラメトリック検定法であり、t分布が直接、もとの平均や標準偏差にはよらない（ただし自由度による）ことを利用している。2組の標本について平均に有意差があるかどうかの検定などに用いられる。統計的仮説検定の一つ。

何のことかさっぱり分かりませんよね。でも安心してください、要するにExcelにデータを入れて計算させて、計算結果のある数値「p値」（ぴーち。英語だとp-value）だけを見て、統計学的に見て本当に改善されたと言えるかどうかを判定できれば良いのです。

統計学的に見て本当に改善されたと言えることを業界用語で「有意差がある」といいます。あるいは差が有意である、と言ったりします。つまり意味のある差が生じているということです。

有意差あり、となったら、皆さんはプレゼンや報告書で、「T検定により統計学的に改善されたことが証明されました」と言う事ができます。これで、統計を知らない人が見れば、大抵圧倒されてしまい、「なるほど、それはすごい」と簡単に納得してくれます。

皆さんやプレゼンや報告書を見る人が統計学に精通している必要はありません。ただ利用するだけで「虎の威を借る」状態にすれば良いのです。

T検定の具体例

ExcelでＴ検定を実施するには、「T.TEST」関数を利用するのが簡単です。T.TESTは次のように計算します。

=T.TEST(改善前のデータ範囲, 改善後のデータ範囲, 2, 1)

この計算結果がp値です。

p値が0.05より小さければ、「有意差あり」すなわち改善効果があったと翻訳します。

また、p値が0.05以上であれば、「有意差なし」すなわち改善効果がなかったことと翻訳します。

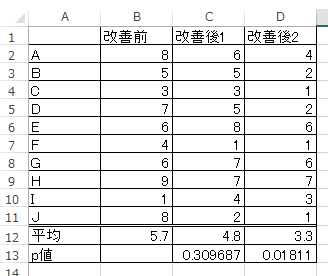
下図の具体例では改善前と改善後で10個のデータを比較しています。改善後１の例では、平均値は5.7から4.8に下がったのですが、p値は0.30程度であり0.05以上ですので、すなわち「有意差なし」、統計学的には改善効果がなかったということです。平均は１近く下がったのですが、統計学的にはたまたまという判断です。

一方、改善後２の例ではp値は0.018程度まで下がり、0.05より小さいですので、すなわち「有意差あり」、統計学的に改善効果があったと言えます。