目次
テストマーケティング
同じ商品でもパッケージのデザインによって売れ行きが変わったり、Webサイトでいえばデザインによってクリック数が変わったりします。
このため、どのデザインにしたら良いか会議があり話し合うのですが、最後は多数決とかエイヤーで直感頼みで決めたり、偉い人の鶴の一声で決めたりする訳です。そこにはこれといった根拠や理由はありません。ただ単になんとなく、決まるのです。
しかし、それでは博打と同じで、特に大きな投資となる場合には、心もとないですし、選ばれなかったデザインを推していた人も釈然としません。
そこでテストマーケティングしてみよう、という話になります。例えば4パターンのデザイン全てのパッケージによる商品を店頭に並べてみたり、Webサイトのデザインを一定期間で変えたりして、どちらが選ばれるのか?というのを検証する訳です。
そうするとデータが取得できます。A/B/C/Dの4パターンのパッケージ商品がそれぞれいくつ売れたのか?とか、A/B/C/Dの4パターンのWebデザインのそれぞれで目的となるリンクやボタンのクリックが何回あったのか?というデータです。
例えば下記のような感じです。
A・・・20個売れた
B・・・30個売れた
C・・・40個売れた
D・・・10個売れた
これはもう圧倒的にCですよね、一番売れたし、となります。
ここで疑い深い人から「本当にそうか?」「たまたまでは?」という疑念が沸き起こります。
そんなときに使うのが、「カイ二乗(かいじじょう)検定」です。
カイ二乗検定とは
カイ二乗検定の「カイ」はギリシャ文字のΧです。英字のエックスに似てますが、ちょっと違います。Χの二乗だからカイ二乗です。
検定とは統計学界隈で使われている手法で、統計学的が裏付けのある意味のある違い(変化)が認められるかどうかを調べるやり方です。検定は、実際には難しい数式による計算を行う必要があるのですが、そういったことは専門家に任せておいて、私たちは要するにビジネスの現場でツールとして検定を使えれば良いのです。
計算自体はExcelに用意されている関数を使うだけです。この関数に数値をいれて、計算結果だけを使います。検定の計算結果はp値(ぴーち)と呼ばれていて、このp値の大きさが5%(0.05)より大きいか・小さいかで判定します。
5%(0.05)より大きければ、有意な(意味のある)違いが無い、と判定されて、上記の例ではパターンCがもっとも売れたのはたまたまで、統計学的な根拠無し、となります。
5%(0.05)より小さければ、有意な(意味のある)違いがある、と判定されて、上記の例ではパターンCがもっとも売れたのは確かで、統計学的な根拠有り、となります。
そして統計学的な根拠有りとなったら、そのことを上司なりクライアントなりにアピールしましょう。上司やクライアントはたいていの場合統計学に明るくないので、「そうなのかー」と納得してくれます。(たまに専門家の方がいて、冷や汗をかきますが)
Excelを使った分析のやり方
Excelでカイ二乗検定はCHITEST()という関数を使います。
まず下図のような表にデータを入れます。2行目はそれぞれのパターンの実測値を、3行目には期待値を入れます。期待値は本来どのパターンも同じになるはずですので、25ということになります。
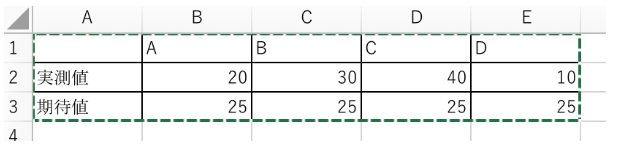
それでどこかのセルに「=CHITEST(B2:E2,B3:E3)」と入れて計算させます。B2:E2というのが実測値の範囲、B3:E3というのが期待値の範囲の指定です。
上記の例では、計算結果は「0.00016974」と出ます。すなわちp値が5%(0.05)より小さいですので、有意であるということになり、従って統計学的にもパターンCがもっとも売れるパターンであると結論づけることができます。
今回サンプル数が全体で100でしたが、100程度はないと「たまたま」との違いを検知できないようですので、注意が必要ですね。
以上、テストマーケティングの効果を統計的に分析する方法について、でした。
統計学の基本が勉強したいときには、この本がお勧めですよ。私も愛読しています。
━━…━━…━━…━━…━━…━━
サンクプランズ・コンサルティング
━━…━━…━━…━━…━━…━━
個人・中小事業者のお客様を対象に会計サービス、コンサルティング、デジタルコンテンツ販売、セミナーなどを行っています。

